L’antenne MIMO transparente et flexible proposée a également été fabriquée et testée pour vérifier ses performances simulées. Chiffre 6a montre le prototype fabriqué, et la Fig. 6b affiche les paramètres de diffusion mesurés. Les résultats indiquent que les paramètres de diffusion simulés et mesurés sont en bon accord. Cependant, il existe quelques légers écarts dans les courbes de fréquence de résonance et de coefficient de transmission des deux éléments d’antenne. Ces écarts peuvent être dus à la tolérance pratique dans les environnements de simulation et de mesure, ainsi qu’à des connexions de soudure imparfaites.
(un) Prototype fabriqué de l’antenne MIMO transparente proposée, (b) paramètres de diffusion mesurés pour l’antenne MIMO transparente et flexible proposée.
Diagramme de rayonnement de l’antenne MIMO transparente à 4,5 GHz (un) Avion E, (b) Plan H.
Les performances ECC et DG de l’antenne MIMO transparente et flexible (un) simulé, (b) mesuré.
En plus de l’analyse précédente, l’antenne MIMO transparente proposée est évaluée pour ses performances à l’aide de mesures telles que le diagramme de rayonnement, le coefficient de corrélation d’enveloppe (ECC), la perte de capacité de canal (CCL), le coefficient de réflexion active totale et le gain effectif moyen (MEG). .
Motif de radiation
Chiffre 7 affiche les diagrammes de rayonnement simulés et mesurés dans les deux plans orthogonaux à 4,5 GHz pour l’un des éléments de l’antenne patch transparente.
L’élément d’antenne patch transparent présente de bonnes performances de rayonnement à 4,5 GHz, avec un gain de 3,2 dB, une efficacité de rayonnement de 61 % et une efficacité totale de 63 %. C’est assez impressionnant pour un élément d’antenne transparent et flexible. Le \(2^{nd}\) un élément étroitement espacé présente également des performances de rayonnement similaires.
Coefficient de corrélation d’enveloppe (ECC) et gain de diversité (DG)
Le coefficient de corrélation d’enveloppe (ECC) est utilisé pour évaluer l’effet du couplage entre les éléments d’antenne, en mesurant la corrélation entre eux dans un système de diversité MIMO. Des performances de gain de diversité plus élevées sont associées à une valeur ECC inférieure qui devrait être inférieure à 0,517. Les performances ECC d’une antenne MIMO peuvent être calculées grâce aux paramètres de diffusion18ou via des modèles de champ lointain19. L’équation suivante (2) est utilisé pour calculer l’ECC à l’aide des paramètres S
$$\begin{aligné} \rho = \frac{\left| S_{11} S_{12}+S_{21} S_{22}\right| ^2}{\left( 1-\left( \left| S_{11}\right| ^2+\left| S_{21} \right| ^2\right) \right) \left( 1-\left ( \left| S_{22} \right| ^2+\left| S_{12}\right| ^2 \right) \right) } \end{aligned}$$
(2)
L’ECC peut également être calculé à l’aide de modèles de champ lointain à l’aide de l’équation suivante. (3) mentionné dans19
$$\begin{aligné} \rho _e=\frac{\left| \iint _{4 \pi }\gauche[ \textbf{E}_1(\theta , \phi ) \cdot \textbf{E}_2(\theta , \phi ) d \Omega \right] \droite| ^2}{\iint _{4 \pi }\left| \textbf{E}_1(\theta , \phi )\right| ^2 d \Omega \iint _{4 \pi }\left| \textbf{E}_2(\theta , \phi )\right| ^2 d \Omega}\end{aligned}$$
(3)
Où le produit des deux champs électriques sur le numérateur peut être donné par l’équation. (4).
$$\begin{aligné} \textbf{E}_1(\theta, \phi) \cdot \textbf{E}_2(\theta, \phi)=E_{\theta 1}(\theta, \phi) E_ {\theta 2}^*(\theta, \phi )+E_{\phi 1}(\theta, \phi ) E_{\phi 2}^*(\theta, \phi ) \end{aligned}$$
(4)
L’équation suivante. (5) est utilisé pour calculer le gain de diversité d’une antenne MIMO19.
$$ Diversité\;Gain(DG) = 10 \times \sqrt {1 – |ECC|^{2} } $$
(5)
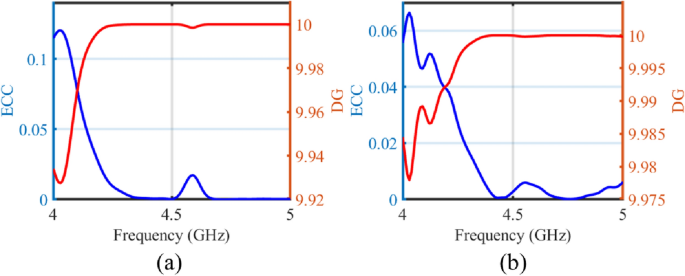
Chiffre 8 affiche les performances d’ECC et de gain de diversité simulées et mesurées de l’antenne MIMO transparente et flexible proposée à l’aide de paramètres de diffusion, qui atteignent une valeur ECC inférieure à 0,005 et une valeur correspondante de 10 pour DG dans la bande de fréquences de fonctionnement souhaitée. L’ECC est également calculé à l’aide de modèles de champ lointain et ses valeurs sont de 0,107 à 4,5 GHz tandis que sa valeur est de 0,157 et 0,163 à 4,41 et 5,56 GHz, respectivement à la fréquence centrale et aux fréquences extrêmes de la bande de fréquences pour \(-\)Bande passante d’impédance de 10 dB. Ces valeurs ECC sont légèrement supérieures aux valeurs ECC calculées à l’aide des paramètres de diffusion, mais elles restent bien inférieures à la valeur minimale requise de 0,5 pour l’ECC.17.
Coefficient de réflexion active totale (TARC) et perte de capacité du canal (CCL)
TARC souligne l’importance de la stabilité de la fréquence de résonance même dans les situations où la différence de phase entre les éléments d’antenne varie17. D’après l’équation. (6) ci-dessous, ce facteur peut être calculé en prenant la racine carrée du rapport entre la puissance disponible moins la puissance rayonnée et la puissance totale disponible.
$$\begin{aligned} \Psi _a^t = \sqrt{\frac{(\text {puissance disponible} – \text {puissance rayonnée})}{\text {puissance disponible}}} \end{aligned}$ $
(6)
Dans les équations. (7) et (8), relation TARC17 avec les paramètres S mesurés est décrit comme :
$$\begin{aligned} \Gamma _a^t = \frac{\sqrt{\sum _{i=1}^N \left| b_i \droit| ^2}}{\sqrt{ \sum _{i=1}^N \left| a_i \right| ^2}} \end{aligné}$$
(7)
où \(b=Dans\) dans l’équation ci-dessus.
$$\begin{aligné} \Gamma _a^t = \sqrt{\frac{\left| S_{11} +S_{12}e^{j\theta }\right| ^2 + \gauche| S_{21}+S_{22}e^{j\theta } \right| ^2 }{2}} \end{aligned}$$
(8)
où \(\thêta \) représente la phase d’alimentation en entrée.
Chiffre 9a présente les performances TARC pour le port 1 de l’antenne MIMO transparente et flexible proposée, qui est \(-\)15 dB à 4,5 GHz. TARC est également calculé en considérant d’autres vecteurs d’excitation avec une variation de phase de 0 à 180 degrés et illustré sur la Fig. 9b. La courbe TARC du port 1 reste quasiment inchangée en raison de ces variations de phase. Des courbes TARC similaires sont observées pour le port 2, cependant, les courbes TARC pour le port 2 ne sont pas présentées ici par souci de concision.
(un) TARC simulé et mesuré pour le port 1 avec un angle de phase de 0 degré, (b) TARC mesuré pour le port 1 avec différents angles de phase du port homologue de 0 à 180 degrés.
CCL, performances pour l’antenne MIMO transparente et flexible proposée.
La métrique CCL est utilisée pour quantifier la perte du nombre de bits de données par seconde et par Hertz via un canal de communication.17.
Chiffre dix décrit les performances CCL de l’antenne MIMO transparente et flexible proposée, indiquant que la valeur CCL reste inférieure à 0,04 bps/Hz dans la bande de fréquence souhaitée. L’équation ci-dessous. (9) est utilisé pour calculer le CCL17 paramètre:
$$\begin{aligned} CCL= – log_2 ^ {|\psi ^\textit{R}|} \end{aligned}$$
(9)
où \(|\psi ^\textit{R}|\) = [\(\rho _{ij}\)], (je,j) \(\epsilon \) (1,2)
alors que \(\rho _{ij}\) est représenté comme suit :
$$\begin{aligned} \rho _{11}= & {} {(1-|S_{11}|^2-|S_{12}|^2)} \end{aligned}$$
(dix)
$$\begin{aligned} \rho _{22}= & {} {(1-|S_{21}|^2-|S_{22}|^2)} \end{aligned}$$
(11)
$$\begin{aligned} \rho _{12}= & {} {(S^*_{11}S_{12} – S^*_{21}S_{22})} \end{aligned}$ $
(12)
$$\begin{aligned} \rho _{21}= & {} {{(S^*_{22}S_{21} + S^*_{12}S_{11})}} \end{aligned }$$
(13)
Une analyse comparative des travaux proposés avec des travaux similaires récents et antérieurs est également présentée dans le tableau 3. On peut constater que l’antenne MIMO transparente et flexible proposée, même avec des éléments d’antenne rapprochés, a démontré des performances comparables avec un espacement considérablement réduit entre les éléments d’antenne par rapport à d’autres travaux similaires.
->Google Actualités
